Earth Seismology: novembre 2010

Time shift of signal using FFT in matlab:
Let's start with the properties of the fourier trasform:

An integrable function is a function ƒ on the real line that is Lebesgue-measurable and satisfies

$\int_{-\infty}^\infty |f(x)| \, dx < \infty.$

Basic properties

Given integrable functions f(x), g(x), and h(x) denote their Fourier transforms by $\hat{f}(\xi)$ , $\hat{g}(\xi)$ , and $\hat{h}(\xi)$ respectively. The Fourier transform has the following basic properties (Pinsky 2002).

Linearity: For any complex numbers a and b, if h(x) = aƒ(x) + bg(x), then $\hat{h}(\xi)=a\cdot \hat{f}(\xi) + b\cdot\hat{g}(\xi).$
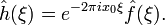
Translation: For any real number x₀, if h(x) = ƒ(x − x₀), then $\hat{h}(\xi)= e^{-2\pi i x_0\xi }\hat{f}(\xi).$
Modulation: For any real number ξ₀, if h(x) = e^2πixξ₀ƒ(x), then $\hat{h}(\xi) = \hat{f}(\xi-\xi_{0})$ .
Scaling: For a non-zero real number a, if h(x) = ƒ(ax), then $\hat{h}(\xi)=\frac{1}{|a|}\hat{f}\left(\frac{\xi}{a}\right)$ . The case a = −1 leads to the time-reversal property, which states: if h(x) = ƒ(−x), then $\hat{h}(\xi)=\hat{f}(-\xi)$ .
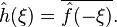
Conjugation: If $h(x)=\overline{f(x)}$ , then $\hat{h}(\xi) = \overline{\hat{f}(-\xi)}.$; In particular, if ƒ is real, then one has the reality condition $\hat{f}(-\xi)=\overline{\hat{f}(\xi)}.$; And if ƒ is purely imaginary, then $\hat{f}(-\xi)=-\overline{\hat{f}(\xi)}.$
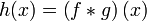Convolution: If $h(x)=\left(f*g\right)(x)$ , then $\hat{h}(\xi)=\hat{f}(\xi)\cdot \hat{g}(\xi).$

We want to use the traslation property of the fourier trasform to shift a signal:

First of all we want to simply fourier trasform the signal X:

TF=fft(X)

Second we have to define the vector of the frequencies used in the exponential that allow the shift:

w=[0:floor((numel(X)-1)/2) -ceil((numel(X)-1)/2):-1]/(Xdelta*numel(X));

where Xdelta is 1/Fs (Fs is the sample frequency of the signal).

We now define a value of the delay in second (accord to our signal in SI):

delay=n;

and we apply the sfhit property of the fft:

TFshifted=TF.exp(-iw*2pidelay)

remember that TF is the fft of the signal X, so a complex function.

We now have the time shifted signal. We want now to build the new signal Xf, that is the correct shifted signal:

n1=ceil(abs(delais)/Xdelta);

where n1 is the first useful sample in the TFshifted function. This value will be used to build the new signal.

We go back in time domain using the inverse fourier trasform:

Xs=real( ifft(TFshifted) );

and if delay <0:

OUTPUT_SIGNAL(1:numel(X)-n1)=Xs(1:numel(X)-ndeb);

else if delay >0:

OUTPUT_SIGNAL(ndeb:numel(X))=Xs(ndeb:numel(X));

Here a complete history of the command:

X=signal %signal to shift
Fs=nn %sample frequency
Xdelta=1/Fs
delay=n;
TF=fft(X);
w=[0:floor((numel(X)-1)/2) -ceil((numel(X)-1)/2):-1]/(Xdeltanumel(X));

TFshifted=TF.exp(-iw2pidelay)
n1=ceil(abs(delay)/Xdelta);
Xs=real( ifft(TFshifted) );
if delay <0:
OUTPUT_SIGNAL(1:numel(X)-n1)=Xs(1:numel(X)-n1);
elseif delay >0:
OUTPUT_SIGNAL(n1:numel(X))=Xs(n1:numel(X));  end

HERE A USEFUL FUNCTION THAT YOU CAN DIRECTLY USE:

function z=FFTshift(signal,delay,sample_Frequency);
% Created by Piero Poli polipiero85@gmail.com

X=signal; %signal to shift
Fs=sample_Frequency; %sample frequency
Xdelta=1/Fs;

TF=fft(X);
w=[0:floor((numel(X)-1)/2) -ceil((numel(X)-1)/2):-1]/(Xdeltanumel(X));

TFshifted=TF.exp(-iw2pidelay);
n1=ceil(abs(delay)/Xdelta);
Xs=real( ifft(TFshifted) );
if delay <0
OUTPUT_SIGNAL(1:numel(X)-n1)=Xs(1:numel(X)-n1);
elseif delay>0
OUTPUT_SIGNAL(n1:numel(X))=Xs(n1:numel(X));
end

z=OUTPUT_SIGNAL;

the code was tested using a simple dirac function and define the Fs=1. Both positive and negative shift were realized. Some problem are coming out in case of delay similar to the lenght of the signal. The shape of the shifted function is really simila to the input signal, no problem of amplitude are documentated. Some little oscillation can be present in case of really simple function (as dirac pulse), this are due to the fft algorithm in matlab and residual imaginary part from the fourier trasform.

If you want to try it use:

signal=zeros(1,1000);

signal(500)=100;

z=FFTshift(signal,-100,1); %negative delay

z=FFTshift(signal,100,1); %positive delay

The pytho tools for seismology

OBSPY (http://www.obspy.org/) is an open-source project dedicated to provide a Python framework for processing seismological data. It provides parsers for common file formats and seismological signal processing routines which allow the manipulation of seismological time series (see Beyreuther et. al. 2010).
The goal of the ObsPy project is to facilitate rapid application development for seismology.

A great tutorial page, help us to use this tools for our seismological analysis.

Why we have to switch to this Python based tools? The graphical power is really strong in Python, really better than matlab, and also is a free open source tools, that include the instruments for various kind of analysis

Earth Seismology

Pagine

lunedì 1 novembre 2010

Time shift of signal using FFT in matlab

Basic properties

We want to use the traslation property of the fourier trasform to shift a signal:

First of all we want to simply fourier trasform the signal X:

TF=fft(X)

Second we have to define the vector of the frequencies used in the exponential that allow the shift:

w=[0:floor((numel(X)-1)/2) -ceil((numel(X)-1)/2):-1]/(Xdelta*numel(X));

where Xdelta is 1/Fs (Fs is the sample frequency of the signal).

We now define a value of the delay in second (accord to our signal in SI):

delay=n;

and we apply the sfhit property of the fft:

TFshifted=TF.exp(-iw*2pidelay)

remember that TF is the fft of the signal X, so a complex function.

We now have the time shifted signal. We want now to build the new signal Xf, that is the correct shifted signal:

n1=ceil(abs(delais)/Xdelta);

where n1 is the first useful sample in the TFshifted function. This value will be used to build the new signal.

We go back in time domain using the inverse fourier trasform:

Xs=real( ifft(TFshifted) );

and if delay <0:

OUTPUT_SIGNAL(1:numel(X)-n1)=Xs(1:numel(X)-ndeb);

else if delay >0:

OUTPUT_SIGNAL(ndeb:numel(X))=Xs(ndeb:numel(X));

Here a complete history of the command:

HERE A USEFUL FUNCTION THAT YOU CAN DIRECTLY USE:

If you want to try it use:

signal=zeros(1,1000);

signal(500)=100;

z=FFTshift(signal,-100,1); %negative delay

z=FFTshift(signal,100,1); %positive delay

Python for Seismology

Pagine

lunedì 1 novembre 2010

Time shift of signal using FFT in matlab

Basic properties

We want to use the traslation property of the fourier trasform to shift a signal:

First of all we want to simply fourier trasform the signal X:

TF=fft(X)

Second we have to define the vector of the frequencies used in the exponential that allow the shift:

w=[0:floor((numel(X)-1)/2) -ceil((numel(X)-1)/2):-1]/(Xdelta*numel(X));

where Xdelta is 1/Fs (Fs is the sample frequency of the signal).

We now define a value of the delay in second (accord to our signal in SI):

delay=n;

and we apply the sfhit property of the fft:

TFshifted=TF.*exp(-i*w*2*pi*delay)

remember that TF is the fft of the signal X, so a complex function.

We now have the time shifted signal. We want now to build the new signal Xf, that is the correct shifted signal:

n1=ceil(abs(delais)/Xdelta);

where n1 is the first useful sample in the TFshifted function. This value will be used to build the new signal.

We go back in time domain using the inverse fourier trasform:

Xs=real( ifft(TFshifted) );

and if delay <0:

OUTPUT_SIGNAL(1:numel(X)-n1)=Xs(1:numel(X)-ndeb);

else if delay >0:

OUTPUT_SIGNAL(ndeb:numel(X))=Xs(ndeb:numel(X)); Here a complete history of the command:

HERE A USEFUL FUNCTION THAT YOU CAN DIRECTLY USE:

If you want to try it use:

signal=zeros(1,1000);

signal(500)=100;

z=FFTshift(signal,-100,1); %negative delay

z=FFTshift(signal,100,1); %positive delay

Python for Seismology

TFshifted=TF.exp(-iw*2pidelay)

OUTPUT_SIGNAL(ndeb:numel(X))=Xs(ndeb:numel(X));

Here a complete history of the command: