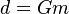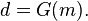more about seismic tomography

Seismic tomography

Seismic tomography is a methodology for estimating the Earth's properties. In the seismology community, seismic tomography is just a part of seismic imaging, and usually has a more specific purpose to estimate properties such as propagating velocities of compressional waves (P-wave) and shear waves (S-wave). It can also be used to recover the attenuation factor Q. Another branch of seismic imaging is seismic migration in which the properties to be estimated include the reflection coefficient or reflectivity.

The simplest case of seismic tomography is to estimate P-wave velocity. Several methods have been developed for this purpose, e.g., refraction traveltime tomography, finite-frequency traveltime tomography, reflection traveltime tomography, waveform tomography.

Seismic tomography is usually formulated as an inverse problem. In refraction traveltime tomography, the observed data are the first-arrival traveltimes t and the model parameters are the velocity v. The forward problem can be formulated as

t = Lv

where L is the forward operator which, in this case, is the raypath matrix. Refraction traveltime tomography is computationally efficient but can only provide a low-resolution image of the subsurface.

To obtain a higher-resolution image one has to abandon the infinite-frequency approximations of ray theory that are applicable to the time of the wave 'onset' and instead measure travel times (or amplitudes) over a time window of some length using cross-correlation. Finite-frequency tomography takes the effects of wave diffraction into account, which makes the imaging of smaller objects or anomalies possible. The raypaths are replaced by volumetric sensitivity kernels, often named 'banana-doughnut' kernels in global tomography, because their shape may resemble a banana, whereas their cross-section looks like a doughnut, with, at least for direct P and S waves, zero sensitivity of the travel time on the geometrical ray path. In finite-frequency tomography, travel time and amplitude anomalies are frequency-dependent, which leads to an increase in resolution.

To exploit the information in a seismogram to the fullest, one uses waveform tomography. In this case, the seismograms are the observed data. In seismic exploration, the forward model is usually governed by the acoustic wave equation. This is an approximation to the elastic wave propagation. Elastic waveform tomography is much more difficult than acoustic waveform tomography. The acoustic wave equation is numerically solved by some numerical schemes such as finite-difference and finite-element methods. Seismic waveform tomography can be efficiently solved by adjoint methods.

Inverse problem

An inverse problem is the task that often occurs in many branches of science and mathematics where the values of some model parameter(s) must be obtained from the observed data.

The inverse problem can be formulated as follows:

Data → Model parameters

The transformation from data to model parameters is a result of the interaction of a physical system, e.g., the Earth, the atmosphere, gravity etc. Inverse problems arise for example in geophysics, medical imaging (such as computed axial tomography and EEG/ERP), remote sensing, ocean acoustic tomography, nondestructive testing, and astronomy.

Inverse problems are typically ill posed, as opposed to the well-posed problems more typical when modeling physical situations where the model parameters or material properties are known. Of the three conditions for a well-posed problem suggested by Jacques Hadamard (existence, uniqueness, stability of the solution or solutions) the condition of stability is most often violated. In the sense of functional analysis, the inverse problem is represented by a mapping between metric spaces. While inverse problems are often formulated in infinite dimensional spaces, limitations to a finite number of measurements, and the practical consideration of recovering only a finite number of unknown parameters, may lead to the problems being recast in discrete form. In this case the inverse problem will typically be ill-conditioned. In these cases, regularization may be used to introduce mild assumptions on the solution and prevent overfitting. Many instances of regularized inverse problems can be interpreted as special cases of Bayesian inference.

General statement of the problem

An inverse problem is to find m such that (at least approximately)

where G is an operator describing the explicit relationship between data d and model parameters m, and is a representation of the physical system. In various contexts, the operator G is called forward operator, observation operator, or observation function.

Linear inverse problems

A linear inverse problem can be described by:

where the forward operator G is a linear operator describing the explicit relationship between data and model parameters, and is a representation of the physical system. In the case of a discrete linear inverse problem describing a linear system, d and m are vectors, and the problem can be written as

where G is a matrix, often called the observation matrix.

Examples

One central example of a linear inverse problem is provided by a Fredholm first kind integral equation.

For sufficiently smooth g the operator defined above is compact on reasonable Banach spaces such as L^p spaces. Even if the mapping is injective its inverse will not be continuous. (However, by the bounded inverse theorem, if the mapping is bijective, then the inverse will be bounded (ie. continuous).) Thus small errors in the data d are greatly amplified in the solution m. In this sense the inverse problem of inferring m from measured d is ill-posed.

To obtain a numerical solution, the integral must be approximated using quadrature, and the data sampled at discrete points. The resulting system of linear equations will be ill-conditioned.

Another example is the inversion of the Radon transform. Here a function (for example of two variables) is deduced from its integrals along all possible lines. This is precisely the problem solved in image reconstruction for X-ray computerized tomography. Although from a theoretical point of view many linear inverse problems are well understood, problems involving the Radon transform and its generalisations still present many theoretical challenges with questions of sufficiency of data still unresolved. Such problems include incomplete data for the x-ray transform in three dimensions and problems involving the generalisation of the x-ray transform to tensor fields.

Non-linear inverse problems

An inherently more difficult family of inverse problems are collectively referred to as non-linear inverse problems.

Non-linear inverse problems have a more complex relationship between data and model, represented by the equation:

Here G is a non-linear operator and cannot be separated to represent a linear mapping of the model parameters that form m into the data. In such research, the first priority is to understand the structure of the problem and to give a theoretical answer to the three Hadamard questions (so that the problem is solved from the theoretical point of view). It is only later in a study that regularization and interpretation of the solution's (or solutions', depending upon conditions of uniqueness) dependence upon parameters and data/measurements (probabilistic ones or others) can be done. Hence the corresponding following sections do not really apply to these problems. Whereas linear inverse problems were completely solved from the theoretical point of view at the end of the nineteenth century, only one class of nonlinear inverse problems was so before 1970, that of inverse spectral and (one space dimension) inverse scattering problems, after the seminal work of the Russian mathematical school (Krein, Gelfand, Levitan, Marchenko). A large review of the results has been given by Chadan and Sabatier in their book "Inverse Problems of Quantum Scattering Theory" (two editions in English, one in Russian).

In this kind of problems, data are properties of the spectrum of a linear operator which describe the scattering. The spectrum is made of eigenvalues and eigenfunctions, forming together the "discrete spectrum", and generalizations, called the continuous spectrum. The very remarkable physical point is that scattering experiments give information only on the continuous spectrum, and that knowing its full spectrum is both necessary and sufficient in recovering the scattering operator. Hence we have invisible parameters, much more interesting than the null space which has a similar property in linear inverse problems. In addition, there are physical motions in which the spectrum of such an operator is conserved as a consequence of such motion. This phenomenon is governed by special nonlinear partial differential evolution equations, for example the Korteweg–de Vries equation. If the spectrum of the operator is reduced to one single eigenvalue, its corresponding motion is that of a single bump that propagates at constant velocity and without deformation, a solitary wave called "soliton".

A perfect signal and its generalizations for the Korteweg–de Vries equation or other integrable nonlinear partial differential equations are of great interest, with many possible applications. This area has been studied as a branch of mathematical physics since the 1970s. Nonlinear inverse problems are also currently studied in many fields of applied science (acoustics, mechanics, quantum mechanics, electromagnetic scattering - in particular radar soundings, seismic soundings and nearly all imaging modalities).

Banana Doughnut theory

The Banana Doughnut theory is a model in Seismic tomography that describes the shape of the Fresnel zone along the entire ray path. This theory suggests that the area that influences the ray velocity is the surrounding material and not the infinitesimally small ray path. This surrounding material forms a tube enclosing the ray but does not incorporate the ray path itself.

This theory gets the name "banana" because tube of influence along the entire ray path from source to receiver is an arc resembling the fruit. The "doughnut" part of the name comes from the ring shape of the cross-section. The ray path is a hollow banana, or a banana-shaped doughnut. An image can be found here: [1]

This theory is sometimes known as "Born-Fréchet kernel theory".