Dal vangelo secondo Maxwell

Nel principio Iddio creò i cieli e la terra. E la terra era informe e vuota, e le tenebre coprivano la faccia dell'abisso, e lo spirito di Dio aleggiava sulla superficie delle acque. E Dio disse:

E la luce fu...

Fast Fourier Trasform: matlab

La trasformata di Fourier veloce (spesso indicata come FFT, dall'inglese Fast Fourier Transform) è un algoritmo ottimizzato per calcolare la trasformata discreta di Fourier (detta DFT) e la sua inversa. La FFT è di grande importanza per una grande varietà di applicazioni, dall'elaborazione di segnali digitali alla soluzione di equazioni differenziali alle derivate parziali agli algoritmi per moltiplicare numeri interi di grandi dimensioni.
Sia x₀, ..., x_N-1 una n-pla di numeri complessi. La DFT è definita dalla formula

per q = 0, 1, ..., N-1

Calcolare direttamente questa somma richiede una quantità di operazioni aritmetiche O(N²). Un algoritmo FFT ottiene lo stesso risultato con un numero di operazioni O(n log(n)). In generale questi algoritmi si basano sulla fattorizzazione di N, ma esistono algoritmi FFT per qualunque N, anche per numeri primi (questi ci piacciono di più).
Poiché l'antitrasformata discreta di Fourier è uguale alla DFT, ma con esponente di segno opposto e 1/N a fattore, qualsiasi algoritmo FFT può essere facilmente invertito.

L'utilizzo della FFT in programmazione, richiede la conoscenza di alcune basi (veramente semplici) dei segnali in frequenza. Ci concentriamo qua sulla descrizione di una semplice funzione che calcoli la FFT di una serie di dati.

Dopo questa semplice intro sulla FFT, ecco una funzione in matlab abile di calcore e plottare i dati trasformati in frequenza. Gli input da fornire sono il vettore dati e la frequenza di campionamento. L'utilizzo della funzione è semplicissimo, sia V il vettore dati e Fs la frequenza di campionamento, si digiti:

z=calcFFT(V,Fs,type)

type è un indice da 1 a 4 che permette di scegliere il tipo di output:

1) plot amplitude  

2) plot phase       

3) plot aplitude and phase (using subplot)       

4) power spectral density

Il codice utilizzato, è molto semplcie, basta salvarlo con estension .m ed aggiungere la directory dove si trova il codice al path di matlab. Ed ecco fatto un semplice programmino che calcoli e plotti la FFT per una qualsiasi serie di dati, e ci dia in automatico il plot di questi.

CODICE:

%% computation and direct plotting of fft
% input parameters:
%
%   signal= input signal to trasform
%   Fs= sample frequency
%   type= 1) plot amplitude
%         2) plot phase
%         3) plot aplitude and phase (using subplot)
%         4) power spectral density
%


function z=calcFFT(signal,Fs,type);




z=fft(signal);

F=(0:(numel(signal))-1)*Fs/numel(signal);

if nargin<3
 type=1;  
end

if type==1
plot(F,abs(z));
xlim([0 Fs/2])
xlabel('Frequency (hz)')
ylabel('Amplitude')
end

if type==2
  plot(F,imag(z));
xlim([0 Fs/2])
xlabel('Frequency (hz)')
ylabel('Phase')
end

if type==3
  subplot(121)
    plot(F,imag(z));
xlim([0 Fs/2])
xlabel('Frequency (hz)')
ylabel('Phase')
  subplot(122)
plot(F,abs(z));
xlim([0 Fs/2])
xlabel('Frequency (hz)')
ylabel('Amplitude')

end  

if type==4
plot(F,abs(z).^2);
xlim([0 Fs/2])
xlabel('Frequency (hz)')
ylabel('Energy')
title('Power spectral density')
end   

MORE: Algoritmo di Cooley-Tukey

L'algoritmo FFT più diffuso è l'algoritmo di Cooley-Tukey. Questo algoritmo si basa sul principio di divide et impera, e spezza ricorsivamente una DFT di qualsiasi dimensione N con N numero composto tale che N=N₁N₂ in DFT più piccole di dimensioni N₁ e N₂, insieme a O(n) moltiplicazioni per l'unità immaginaria, detti fattori twiddle.
Questo metodo (e in generale l'idea di una trasformata di Fourier veloce) fu reso popolare da una pubblicazione di James William Cooley e John Wilder Tukey nel 1965, ma in seguito si scoprì che i due autori avevano indipendentemente reinventato un algoritmo noto a Carl Friedrich Gauss nel 1805 (e successivamente riscoperto in molte altre forme limitate).
L'uso più conosciuto dell'algoritmo di Cooley-Tukey è di dividere e trasformare in due pezzi di n/2 ad ogni passo, ed è quindi ottimizzato solo per dimensioni che siano potenze di due, ma in generale può essere utilizzata qualsiasi fattorizzazione (com'era noto sia a Gauss che a Cooley e Tukey). Questi casi sono chiamati rispettivamente casi radice di 2 e radice mista (e le altre varianti hanno i propri nomi. Anche se l'idea di base è ricorsiva, la gran parte delle implementazioni tradizionali riorganizzano l'algoritmo per evitare la ricorsione esplicita. Inoltre, poiché l'algoritmo di Cooley-Tukey spezza la DFT in DFT più piccole, può essere arbitrariamente combinato con qualsiasi altro algoritmo per la DFT.

Altri algoritmi per calcolare la FFT 

Ci sono altri algoritmi per la FFT oltre al Cooley-Tukey. Per N=N₁N₂ con N₁ e N₂ numeri coprimi può essere utilizzato l'algoritmo di Good-Thomas PFA (Prime-factor FFT Algorithm), basato sul teorema cinese del resto, che fattorizza la DFT in un modo simile al Cooley-Tukey. L'algoritmo FFT di Rader-Brenner è un sistema di fattorizzazione simile al Cooley-Tukey ma con fattori twiddle immaginari puri, riducendo il numero delle moltiplicazioni al costo di un aumento delle addizioni e della instabilità numerica.
Gli algoritmi che suddividono ricorsivamente la DFT in operazioni più piccole diverse dalla DFT includono l'algoritmo di Bruun e il QFT. (Gli algoritmi di Rader-Brenner e il QFT sono stati proposti per dimensioni che siano potenze di 2, ma è possibile che vengano adattati per numeri composti qualunque. L'algoritmo di Bruun si può applicare su dimensioni qualunque anche composte). In particolare l'algoritmo per la FFT di Bruun è basato sull'interpretare la FFT come la fattorizzazione ricorsiva del polinomio zⁿ-1 in polinomi a coefficienti reali nella forma z^m-1 e z^2m+az^m+1.
Un altro punto di vista polinomiale è sfruttato dall'algoritmo FFT di Winograd, che fattorizza zⁿ-1 in polinomi ciclotomici, che spesso hanno coefficienti 1, 0 o −1, e quindi richiedono poche (se non nessuna) moltiplicazione, quindi può essere utilizzato per ottenere FFT con un numero minimo di moltiplicazioni ed è spesso usato per trovare algoritmi efficienti per piccoli fattori. In effetti Winograd dimostrò che la DFT può essere calcolata con solo O(n) moltiplicazioni; sfortunatamente questo si ottiene con un numero considerevolmente superiore di addizioni, uno scambio non più favorevole sui moderni processori dotati di chip dedicati per le moltiplicazioni in virgola mobile. In particolare, l'algoritmo di Winograd fa anche uso dell'algoritmo PFA e di quello di Rader per le FFT con dimensioni che siano numeri primi.
Un altro algoritmo FFT per numeri primi è dovuto a L. I. Bluestein ed è a volte chiamata algoritmo chirp-z: riesprime la DFT come una convoluzione, la cui dimensione può essere portata ad una potenza di due e valutata dalla FFT di Cooley-Tukey.

Algoritmi FFT specializzati per dati reali e/o simmetrici 

In molte applicazioni i dati di input per la DFT sono reali puri, nel qual caso il risultato soddisfa la simmetria

e sono stati conseguentemente sviluppati algoritmi FFT per questa situazione (cfr. Sorensen, 1987). Un approccio consiste nel riutilizzare un algoritmo ordinario e rimuovere le parti di calcolo ridondanti, risparmiando approssimativamente un fattore due di occupazione di memoria e di tempo impiegato. In alternativa, è possibile esprimere la trasformata discreta di Fourier di una n-pla con un numero pari di elementi tutti reali come la trasformata discreta complessa della metà della dimensione originaria le cui parti reali ed immaginarie sono gli elementi pari e dispari degli elementi originari, seguiti da O(n) operazioni di post-processo.
Si pensava una volta che le n-ple reali di cui calcolare la DFT potessero essere calcolate in modo più efficiente con la trasformata discreta di Hartley (detta DHT dall'acronimo di Discrete Hartley Transform), ma si scoprì in seguito che in genere possono essere individuati algoritmi FFT specializzati che richiedono meno operazioni del corrispondente algoritmo DHT. Anche l'algoritmo di Bruun fu inizialmente proposto per avvantaggiarsi dei numeri reali come input, ma non è mai diventato popolare.

Accuratezza e approssimazioni

Tutti gli algoritmi FFT presentati finora calcolano esattamente la FFT (in senso aritmetico, trascurando cioè gli errori dovuti ai calcoli in virgola mobile). Tuttavia sono stati anche proposti algoritmi FFT che calcolano la DFT approssimativamente, con un errore che può essere reso arbitrariamente piccolo al costo di un maggiore sforzo computazionale. Questi algoritmi scambiano l'errore di approssimazione a favore di una maggiore velocità od altre caratteristiche. Alcuni esempi sono l'algoritmo FFT di Edelman et al. (1999), la FFT di Guo e Barrus (1996) basata sui wavelet o quella di Shentov et al. (1995).
Anche gli algoritmi FFT "esatti" hanno degli errori quando viene utilizzata l'aritmetica a virgola mobile a precisione finita, ma questi errori sono in genere molto piccoli; la maggior parte degli algoritmi FFT hanno eccellenti proprietà numeriche. Il limite superiore dell'errore relativo per l'algoritmo di Cooley-Tukey è O(ε log n), contro O(ε n^3/2) per la formula originaria della DFT (Gentleman e Sande, 1966). Questi risultati, comunque, sono molto sensibili verso l'accuratezza dei fattori twiddle usati nella FFT (che sono poi i valori delle funzioni trigonometriche), e non è raro che implementazioni poco accurate della FFT abbiano precisione molto peggiori, ad esempio se utilizzano tabelle dei valori trigonometrici poco accurate. Alcuni algoritmi di FFT, come il Rader-Brenner, sono intrinsecamente meno stabili.
In aritmetica a virgola fissa, la precisione degli errori accumulati dagli algoritmi di FFT sono peggiori, e crescenti come O(√n) per l'algoritmo di Cooley-Tukey (Oppenheim & Schafer, 1975). Inoltre, raggiungere questa precisione richiede un'accurata attenzione e nello riscalare i fattori per minimizzare la perdita di precisione, e gli algoritmi di FFT in virgola fissa richiedono il riscalamento ad ogni stadio intermedio delle decomposizioni come nel Cooley-Tukey.
Per verificare la correttezza di un'implementazione di un algoritmo FFT, garanzie rigorose possono essere ottenute in tempo O(n log n) con una semplice procedura che controlla le proprietà di linearità, della risposta impulsiva e della tempo-invarianza per dati in input casuali (Ergün, 1995).

The Wave: The Movie

How to propagate waves in matlab!!!

This extremely simple matlab code, explain how to create a really simple wave propagation simulator in space. It's natural possible to convert this simple code to propagate wave also in space, by simple change of the variable.

The code use the definition of velocity, frequency (converted in pulsation), and amplitude. Here we propagate just 3 waves trains, for which the variable parameter is the wave number. 

This is a really really simple example of how to code the wave propagation, and i didn't spend so muche time in try to write it in elegant way. 

In the last part of the code, there is the most important think (for my point of view). This is an example of how to create a simple movie of the propagative waves.

Here the code:

% Wave propagation movie

%movie(M,20)

clear all
close all
x=linspace(0,10,1000);
c=340;  %velocity
f=50;   % frequency
w=2*pi*f;  %pulsation
k=w/c;     % wavenumber
k1=100*2*pi/c;
k2=80*2*pi/c;

p0=1;      %amplitude
T=1/f;
dT=T/20
Time=[0:dT:dT*500];
n=length(Time);
for t=1:n
   
    p=p0*exp(j*(w*Time(t)-k*x));
    p1=p0*exp(j*(w*Time(t)-k1*x));
    p2=p0*exp(j*(w*Time(t)-k2*x));
  
    figure(1)

    plot(x,p,x,p1,'r',x,p2,'k')
    grid on
ylim([-p0-10 p0+10])
xlim([-0 10])
xlabel('space')

M(:,t)=getframe;
end

movie(M,1)
 

MANTLE CONVECTION (from mantleplumes.org)

Don L. Anderson Seismological Laboratory, California Institute of Technology, Pasadena, CA 91125 dla@gps.caltech.edu

Contained fluids heated from below spontaneously organize into convection cells when sufficiently far from conductive equilibrium. Fluids can also be organized by surface tension, and other forces and structures at the top, and by imposed horizontal temperature gradients and motions. At mantle conditions rocks are generally treated as fluids. Plate tectonics was once regarded as passive motion of plates on top of mantle convection cells but it now appears that continents and plate tectonics organize the flow in the mantle and that the mantle is the passive element. The flow is driven by instability of the cold surface layer and near-surface lateral temperature gradients such as imposed by slabs and continents. Plate tectonics may be a self-driven, far-from-equilibrium system that organizes itself by dissipation (entropy production) in and between the plates. The mantle may simply be a provider of energy and material. The effect of pressure suppresses the role of the lower thermal boundary layer (TBL) at the core-mantle-boundary (CMB) interface. The state of stress in the lithosphere defines the plates, plate boundaries and locations of midplate volcanism. Fluctuations in stress, due to changing boundary conditions, are responsible for global plate reorganizations and evolution of volcanic chains. In Rayleigh-Benard convection, by contrast, temperature fluctuations are the important parameter. In plume theory, plates break where heated or uplifted by plumes. Ironically, the fluid flows in the experiments by Benard, which motivated the theory by Rayleigh, were driven by surface tension, i.e. stresses at the surface.

Mantle convection is quite different from the usual pot-on-a-stove metaphor. A large bowl of several superposed fluids and ice cubes in a microwave oven, programmed to decrease the power with time, would be a better, but still incomplete, analogy. The missing element in laboratory and kitchen experiments, and most computer simulations, is pressure. The mantle is heated from within, cooled from above and cools off with time (secular cooling). All of these effects drive convective motions. The distribution of radioactive elements within the Earth is not uniform. Heating from below is minor, at least for the mantle as a whole. Viscosity varies with depth and temperature. Solid-solid phase changes (some exothermic and some endothermic), occur at various depths. Rheology changes with stress. There are text books, monographs and hundreds of papers on the subject of thermal convection but few are applicable to the mantle. Mantle convection is far from being a closed subject. Computer simulations have not yet included a self-consistent thermodynamic treatment of the effect of temperature, pressure and volume on the physical and thermal properties, and understanding of the “exterior” problem (the surface boundary condition) is in its infancy. Plate tectonics itself is implicated in the surface boundary condition. Melting is an important aspect of real mantle convection. Sphericity, pressure and the distribution of radioactivity break the symmetry of the problem and the top and bottom boundary conditions play quite different roles than in the simple calculations and cartoons of mantle dynamics and geochemical reservoirs. Conventional (Rayleigh-Benard) convection theory may have little to do with plate tectonics. The research opportunities are enormous.

The history of ideas Convection can be driven by bottom heating, top or side cooling, and by motions of the boundaries. Although the role of the surface boundary layer and “slab-pull” are now well understood and the latter is generally accepted as the prime mover in plate tectonics, there is a widespread perception that active hot upwellings from deep in the interior of the planet, independent of plate tectonics, are responsible for “extraordinary” events such as plate reorganization, continental break-up, extensive magmatism and events far away from current plate boundaries. Plate tectonics is considered by some to be an incomplete theory of mantle dynamics. Active upwellings from deep in the mantle are viewed as controlling some aspects of surface tectonics and volcanism, including reorganization, implying that the mantle is not passive. These have been modeled by the injection of hot fluids into the base of a tank of motionless fluid. This is called the plume mode of mantle convection. Numerical experiments show that mantle convection is controlled from the top by continents, cooling lithosphere, slabs and plate motions and that plates not only drive and break themselves but can control and reverse convection in the mantle (1-6). Supercontinents and other large plates generate spatial and temporal temperature variations. The migration of continents, ridges and trenches cause a constantly changing surface boundary condition, and the underlying mantle responds passively (7-10). Plates break up and move, and trenches roll back because of forces on the plates and  interactions of the lithosphere with the mantle. Density variations in the mantle are, by and large, generated by plate tectonics itself, for example through slab cooling, refertization of the mantle, continental insulation, and these also affect the forces on the plates. Surface plates are constantly evolving and reorganizing although major reorganizations are infrequent. They are mainly under lateral compression although local regions having horizontal least-compressive axes may be the locus of dikes and volcanic chains. The mantle is generally considered to convect as a single layer (whole mantle convection) or, at most two (the standard geochemical model). However, the mantle is more likely to convect in multiple layers as a result of gravitational sorting during accretion and the density difference between the mantle products of differentiation.

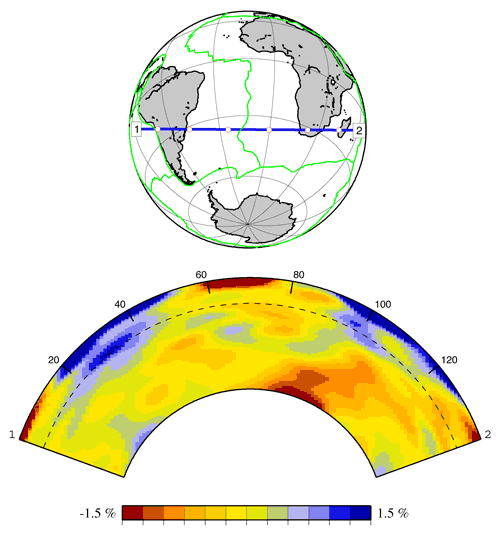Cross section through the whole-mantle tomography model of Ritsema et al. (1999) showing the strong heterogeneity that characterises the upper mantle and the core-mantle boundary region, contrasting with the weak heterogeneity in the mid-mantle. The mantle may be divided into three or more chemically distinct layers.

Boundary Conditions The core has low viscosity and high thermal conductivity so the base of the mantle is in contact with a stress-free isothermal bath. The top boundary condition is plate tectonics. It is not an isothermal, stress-free, homogeneous, uniform boundary condition. If the plates are held together by lateral stress (7-10) then the surface must be free to self-organize, a condition not yet allowed in any simulation. Reorganization means the ability to form new plate boundaries and generate new plates that are consistent with the ever-changing stress state of the lithosphere. In the absence of plates or a high viscosity lid the mantle would experience Rayleigh-Benard convection. Above a critical Rayleigh number fluids spontaneously convect and self-organize. Buoyancy of the fluid, which is dependent on the coefficient of thermal expansion (expansivity) and temperature fluctuations, drives the flow and the viscosity forces of the fluid dissipate the energy. Temperature-dependent viscosity, a semi-rigid lithosphere (held together by lateral compressive stresses) and buoyant continents (and thick crust regions) completely change this. Gravitational forces on cooling plates cause them to move. Dissipation takes place in and between the plates, causing them to self-organize and to organize the underlying weaker mantle. Plate tectonics, to a large extent, is driven by the unstable surface TBL and therefore resembles convection in fluids which are cooled from above (see http://anquetil.colorado.edu/VE/convection.shtml). Pressure decreases the expansivity and Rayleigh number so it is difficult to generate buoyancy or vigorous small-scale convection at the base of the mantle. In addition, heat flow across the CMB is about an order of magnitude less than at the surface so it takes a long time to build up buoyancy. In contrast to the upper TBL, which involves frequent ejections of narrow dense slabs into the interior, the lower TBL is sluggish and does not play an active role in mantle convection. CMB upwellings are expected to be thousands of kilometers in extent and embedded in high-viscosity mantle. Lithospheric architecture and slabs set up lateral temperature gradients that drive small-scale convection. For example, a newly opening ocean basin juxtaposes cold cratonic temperatures of about 1000°C at 100 km depth with asthenospheric temperatures of about 1400°C. This lateral temperature difference sets up convection. Convective flows driven by this mechanism can reach speeds of 15 cm/yr and may explain volcanism at the margins of continents and cratons, and  at oceanic and  continental rifts. Shallow upwellings resulting from this mechanism are intrinsically three-dimensional and plume-like.

Fundamentals Materials usually expand when heated. This causes them to rise when embedded in compositionally similar material. Pressure drives atoms closer together and suppresses the ability of high temperatures to create buoyancy. This is unimportant in the laboratory but it also means that laboratory simulations of mantle convection, including theinjection experiments used to generate plumes, are not relevant to the mantle. Unfortunately, computer simulations are generally used to confirm the laboratory results and, when applied to the mantle, also ignore the effects of pressure on material properties. In fact, the effects of temperature are also generally ignored except the effect of temperature on density. This is called the Boussinesq approximation. This works fine in the laboratory, but does not apply to the mantle. Lateral variations in temperature are what drives thermal convection. Lateral variations in pressure are generally unimportant since the pressure in the material outside of the rising element is about the same as inside. But the increase in pressure with depth means that viscosity, thermal conductivity and expansivity change, making it harder for material to convect. The system responds by increasing the dimensions of the thermal instabilities in order to maintain buoyancy and to overcome viscous resistance. A closed or isolated system at equilibrium returns to equilibrium if perturbed. In a tank of fluid, or the mantle, with a cold surface and a hot bottom, heat will flow by conduction alone unless the temperature gradient gets too large. The stable conduction situation is called equilibrium. A far-from-equilibrium dissipative system, provided with a steady source of energy or matter from the outside world, can organize itself via its own dissipation. It is sensitive to small internal fluctuations and prone to massive reorganization. The fluid in a pot heated on a stove evolves rapidly through a series of transitions with complex pattern formation even if the heating is spatially uniform and slowly varying in time. The stove is the outside source of energy and the fluid provides the buoyancy and the dissipation (via viscosity). Far-from-equilibrium self-organization and reorganization require an open system, a large, steady, outside source of matter or energy, non-linear interconnectedness of system components, dissipation, and a mechanism for exporting entropy products. Under these conditions the system responds as a whole, and in such a way as to minimize entropy production (dissipation). Certain fluctuations are amplified and stabilized by exchange of energy with the outside world. Structures appear which have different time and spatial scales than the energy input). Similar considerations apply to a fluid cooled from above. The cold surface layer organizes the flow and drives the convection. If the fluid has a strongly temperature-dependent viscosity, or if buoyant things are floating on top, only part of the surface layer is able to circulate into the interior. If the upper mantle is near or above the melting point there are other sources of buoyancy and dissipation and the possibility of lubrication. Volcanic chains can form as a result of buoyant dikes breaking through the surface layer at regions of relative extension. Melts are predicted to pond beneath regions of lateral compression.

Plume Type Convection The idea that a deep TBL may be responsible for narrow structures such as volcanic chains is based on heating-from-below experiments and calculations, or injection experiments. The effects of pressure on thermal properties are not considered (the Boussinesq approximation). In the Earth the effects of temperature and pressure on convection parameters cannot be ignored and these must be determined as part of the solution in a self-consistent way. Such calculations, and mantle tomography, suggest that it is highly probable that the mantle below 2,000 km depth, and possibly below 1,000 km depth is isolated from the surface, except by Newton’s and Fourier’s laws. Furthermore, it is the cooling of the mantle that controls the rate of heat loss from the core. The core does not play an active role in mantle convection. The magnitude of the bottom TBL depends on the cooling rate of the mantle, the pressure and temperature dependence of the physical properties and the radioactivity of the deep mantle. The local Rayleigh number of the deep mantle is very low.

Layered mantle convection Chemical boundaries are hard to detect by seismic techniques but the evidence favors one such boundary near 1,000 km. The seismic boundary at an average depth of 650 km is primarily due to a solid-solid phase change, in mantle minerals, with a negative Clapeyron slope. Slabs can be halted at such a boundary but if they accumulate they can punch through. Observations also suggest the presence of one or more chemically distinct layers at the base of the mantle that may extend, in places, as high as 1,000 km from the CMB. This region exhibits large-scale sluggish behavior as appropriate for high Prandt number, low Rayleigh number convection. This kind of chemical and gravitational stratification resolves various geodynamic and geochemical paradoxes and is more consistent with petrology and mineral physics than the one- and two-layer models that are most discussed in the literature. It is generally believed that geochemical observations support models of layered mantle convection and the popular geochemical box models. However, it is chemical heterogeneity that is demonstrated by the data, which cannot determine the depth, size or configurations of the inhomogeneities. Isolated deeper layers that do not currently participate in surface volcanism are sometimes called “hidden”,“stealth” or “phantom” reservoirs. They show up as “missing components” and “geochemical paradoxes”. If pressure is ignored it requires about a 6% increase in intrinsic density for a deep mantle layer to be stable against a temperature-induced overturn. Plausible differences in density between most mantle products of accretional differentiation intermediate in density between the crust and the core are about 1 or 2%, if the variations are due to changes in silicon, aluminum, calcium and magnesium. Changes in iron content can give larger variations. Such density differences have been thought too small to stabilize stratification. However, when pressure is taken into account such slightly denser layers become trapped, although their effect on seismic velocities can be slight. These are therefore “stealth” layers or reservoirs which are below the ability of seismic waves to detect, except by special techniques. Multilayered convection simulations are avoided for the reason that modelers think there is no evidence for it, and the calculations are difficult and time consuming. This is a major hindrance for advances in mantle dynamics and geochemistry and an opportunity for future research. A chemically stratified mantle with variable-depth chemical boundaries near 1,000 and 2,000 km and a lower mantle depleted in radioactive elements appears to satisfy available geochemical and geophysical constraints.

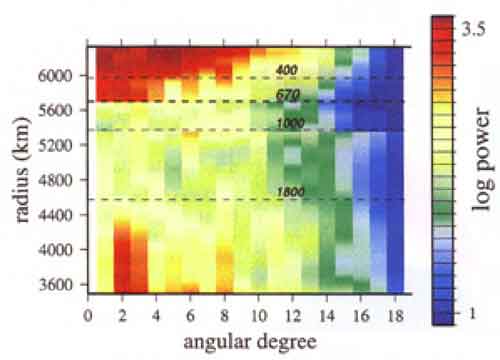Spherical harmonic power spectrum of velocity throughout the mantle (from Gu et al., 2001). The Earth is clearly characterised by strong heterogeneity in the longer-wavelength components in the lithosphere and upper mantle and the lowermost mantle, with little heterogeneity in between. The three major regions of the mantle are evident. There may also be chemically distinct layers at the very base of the mantle (D") and a buoyant, refractory layer at the top of the mantle (the perisphere).

The forces on plates The creation of new plates at ridges, the subsequent cooling of these plates, and their ultimate subduction at trenches introduce forces which drive and break up the plates. They also introduce chemical and thermal inhomogeneities into the mantle. Plate forces such as ridge push, slab pull, and trench suction are basically gravitational forces generated by cooling plates. They are resisted by transform fault, bending and tearing resistance, mantle viscosity and bottom drag. If convection currents dragged plates around, the bottom drag force would be the most important. However, there is no evidence that this is a strong force, and even its sign is unknown (driving or resisting drag). The thermal and density variations introduced into the mantle by subduction also generate forces on the plates. The deep mantle, even if convectively isolated from the upper mantle, affects the elevation and stress state of the lithosphere. Density variations in the mantle also cause variations in elevation and stress in the plate, which are added to the plate forces. Hot regions of the lower mantle will heat the upper mantle and may control, to some extent, the locations of supercontinents and long-lived subduction zones. Even if the mantle is irreversibly chemically stratified into two or more layers, the deep layers will have an effect on geophysical observables. Regions of high elevation, tensile stress and volcanism will tend to be above low-density regions of the deep mantle unless counteracted by gravitational forces in the plates themselves and at plate boundaries. Because of the high viscosity of the deep mantle the warm regions are semi-permanent compared to features in the upper mantle. The large viscosity contrast means that the various layers are more likely, on average, to be thermally coupled than shear coupled. From a tomographic point of view, this means that some mantle structures may appear to be continuous even if the mantle is stratified (see (11) and http://karel.troja.mff.cuni.cz/staff/HANKA_CIZKOVA/Anim/animace.htm).

The core-mantle boundary region The TBL at the base of the mantle generates a potentially unstable situation. The effects of pressure increase the thermal conductivity, decrease the thermal expansion and increase the viscosity. This means that conductive heat transfer from below is more efficient than at the surface, that temperature increases have little effect on density and that any convection will be sluggish. Although the amount of heat coming out of the core may be appreciable, it is certainly less (~10%) than that flowing through the surface. The net result is that lower-mantle upwellings take a long time to develop and they must be very large in order to accumulate enough buoyancy to overcome viscous resistance. The spatial and temporal scale of core-mantle-boundary instabilities are orders of magnitude larger than those at the surface. This physics is not captured in laboratory simulations or calculations that adopt the popular Boussinesq approximation. Pressure also makes it easier to irreversibly chemically stratify the mantle. A small intrinsic density difference due to subtle changes in chemistry can keep a deep layer trapped since it requires such large temperature increases to make it buoyant. Layered mantle convection is the likely outcome.

A Primer on Convection A system cooled from above or heated from within will develop an upper thermal boundary layer which drives the system. The thermal boundary layer (plate, slab) is the only active element. All upwellings are passive, and diffuse. For large Prandtl number (the mantle) the mechanical boundary layers are the size of the mantle. The scale of thermal boundary layers (plate thickness) is controlled by the Rayleigh number (Ra), which for the top is of the order of hundreds of km. Ra is controlled both by physical properties (conductivity, expansivity etc.) and environment (heat flow, temperature gradients etc.). Both these factors cause Ra to be orders of magnitude lower at the base of mantle than at top. Therefore convective vigor is orders of magnitude less at the base of mantle. The mechanical and thermal boundary layers at the base of mantle are therefore of the order of thousands of kilometers in lateral dimensions. Radioactivity does not contribute to unstable superadiabatic gradients because the time constants are much greater than convective time constants.

Notes In the Morgan plume theory, upwellings are the active narrow elements and downwellings are passive and diffuse. This is the exact opposite of cooled-from-above-systems and what the geophysical data tell us. Morgan plume theory holds for systems heated from below and not cooled from above. If there are no pressure effects and if all the heat enters from below and leaves from the top then there is symmetry and both upper and lower TBL are active. Sphericity, pressure, continents and distribution of radioactivity break symmetry and mean that lower TBL instabilities are sluggish and gigantic compared with upper TBL instabilities (slabs). Continents/cratons also contribute to the lateral thermal gradients that drive convection from the top. It is lateral thermal gradients, not vertical ones, that drive convection. The lithosphere, instead of the mantle, controls cooling of mantle.

References M. Gurnis, Nature, 332, 695 (1988). M. Gurnis, S. Zhong, Geophys. Res. Lett., 18, 581 (1991). M. Gurnis, S. Zhong, J. Toth, The history and dynamics of global plate motions, AGU, Geophysical Monograph 121, pp. 73, (2000) J. P. Lowman, G. T. Jarvis, Geophys. Res. Lett., 20, 2087 (1993). J. P. Lowman, G. T. Jarvis, J. Geophys. Res., 104, 12,733 (1999). S. Zhong, M. Gurnis, Geophys. Res. Lett., 22, 981 (1995) Anderson, D. L., Top-down tectonics, Science, 293, 2016 (2001). Anderson, D. L., A statistical test of the two reservoir model for helium, Earth Planet. Sci. Lett., 193, 77 (2001). Anderson, D. L., 2001, How many Plates?, Geology, 30, 411 (2002). Anderson, D. L. Plate Tectonics as a Far- From- Equilibrium Self-Organized System, in Plate Boundary Zones, ed. S. Stein, AGU Monograph, (2002). Cizkova, H., Cadek, O., van den Berg, A.P. and N.J. Vlaar, Can lower mantle slab-like seismic anomalies be explained by thermal coupling between the upper and lower mantles? Geophys. Res. Lett., 26, 1501-1504, 1999. General References Agee, C. B. and Walker, D., Mass balance and phase density constraints on early differentiation of chondritic mantle, Earth Planet. Sci. Lett., 90, 144 (1988). Anderson, D. L., Theory of the Earth, Blackwell Scientific Publications, Boston, pp. 366 (1989). [Chapter 8 is relevant to irreversible stratification of mantle and low U in the lower mantle.] Anderson, D. L., Where on Earth is the Crust?, Physics Today, March 1989, 38-46. (1989). Clark, S. P., and Turekian, K. K., Thermal constraints on the distribution of long-lived radioactive elements in the Earth: Phil. Trans. R. Soc. Lond., 291, 269-275 (1979). Coltice, N., and Ricard, Y., Geochemical observations and one layer mantle convection: Earth Planet. Sci. Lett., 174, 125-137 (1999). Conrad, C. P., and Hager, B. H., Mantle convection with strong subduction zones: Geophys. J. Int., 144, 271-288 (2001). Cordery, M. J., Davies, G. F., and Campbell, I. H., Genesis of flood basalts from eclogite-bearing mantle plumes: J. Geophys. Res., 102, 20,179-20,197 (1997). Cserepes, L., Yuen, D. A., and Schroeder, B. A., Effect of the mid-mantle viscosity and phase-transition structure of 3D mantle convection: Phys. Earth. Planet. Int., 118, 135-148 (2000) Davaille A., Simultaneous generation of hotspots and superswells by convection in a heterogeneous planetary mantle: Nature, 402, 756-760 (1999). Davies, G. F., Dynamic Earth: Plates, Plumes and Mantle Convection: Cambridge University Press, Cambridge, 458 pp. (2000). Gu, Y., A.M. Dziewonski, S. Weijia, and G. Ekstrom, Models of the mantle shear velocity and discontinuities in the pattern of lateral heterogeneities, J. geophys. Res., 106, 11,169-11,199 (2001). King, S. D., and Anderson, D. L., An alternative mechanism of flood basalt formation: Earth Planet. Sci. Lett., 136, 269-279 (1995). Ritsema, J., H.J. van Heijst, and J.H. Woodhouse, Complex shear wave velocity structure imaged beneath Africa and Iceland, Science, 286, 1925-1928 (1999). Schubert, G., Turcotte, D., Olson, P., Mantle convection in the Earth and planets: C. U. Press, 956 pp. (2001). Scrivner, C. and Anderson, D. L., The effect of post Pangea subduction on global mantle tomography and convection: Geophys. Res. Lett., 19, 1053-1056 (1992). Tackley, P. J., Mantle convection and plate tectonics: Toward an integrated physical and chemical theory: Science, 288, 2002-2007 (2000). Tackley, P., Three dimensional simulations of mantle convection with a thermo-chemical basal boundary layer: in: M. Gurnis, M. et al., eds., The Core-Mantle Boundary Region, Washington, AGU, 334 pp. (1998). Turcotte, D.L. and G. Schubert, in Geodynamics, John Wiley & Sons, New York, 450 pp. (1982). Wen, L. and Anderson, D. L., Layered mantle convection: A model for geoid and topography: Earth Planet. Sci. Lett., 146, 367-377 (1997). Wen, L. and Anderson, D. L., Slabs, hotspots, cratons and mantle convection revealed from residual seismic tomography in the upper mantle: Phys. Earth Planet. Int., 99, 131-143 (1997). http://jspc-www.colorado.edu/~szhong/mantle.html

FANTASISMOLOGIA

COME NASCE LA SCIENZA!

Da sempre la dottrina del benpensare, ci ha portato a credere a favole più o meno veritiere, sulle quali basiamo la nostra origine, il nostro futuro ed individuiamo gli obiettivi della nostra vita. Barbuti capelloni, con doti degne di super eroi sono all'origine di una cultura che nei secoli ha fatto e disfatto di tutto, ha abbrustolito chi era scomodo e protetto chi "eticamente" scomodo ma "politicamente" utile. Non vedo perchè non creder quindi alla favola che sto per raccontarvi, per darsi ragione della questione "da dove viene la scienza!??". Parleremo naturalemente di sismologia, ma sotto una ottica leggermente differente dal solito. Scordate le storie che vi hanno raccontato nei corsi universitari, la sismologia che nasce per la localizzazione dei colpi di mortaio!!! Tutte fesserie. La sismologia nasce grazie alla preziosa azione di Danning!

Chi è? Ma come? Che domande sono? Il cattivo di Superman, uno degli acerrimi nemici dell'uomo d'acciao, quello che tutto avrebbe fatto per dominare un mondo fantastico, ma che da sempre ha dovuto fare i conti con lo scomodo kryponiano.

E che c'entra Danning con la sismologia?

Facciamo un passo indietro, nel 1958,  "World's Finest"  n. 93. In questa occasione il signor Victor Danning si ritrova casualmente un livello di intelligenza aumentato (fino a livello genio!!!). Con questo tasso intellettivo estremo, Danning decide di metter in atto una serie di super crimini, tanto che il solo Super Man non se la sente di affrontare la situazione da solo, e si avvale della collaborazione di due esperti del "salvare l'umanità": Batman e Robin.

Il trio riesce più e più volte a sventare per un pelo le malefatte di Dunning, che stufo di essere interrotto sul più bello, attinge alla sua estrema intellingeza temporanea e decide di applicare una soluzione finale: eliminare i tre.

I supereroi non sono però così facili da trovare, sono soliti passare il tempo libero a casa di batman, nella famosa bat-caverna (che dio solo sa dove si trovi). E allora? Dunnig ha l'idea geniale: ordina ad i suoi scagnozzi di disseminare la città di dinamite, e monitorare sul "radar-sismografo" le onde d'urto che si propagano sotto la città, spiegando che la velocità di propagazione di queste sarà ben diversa al momento che passeranno dalla roccia al vuoto della caverna. 

E bravo Danning (spero che Batman non mi abbia sentito), ci hai aperto la strada, ora potremo scoprire pozzi pertroliferi, falde acquifere, tutto questo grazie alla tua intuizione geniale. 

Ed ecco qui una bella favoletta, che a differenza di quelle che tentano di insegnarci la domenica, si basa quantomeno su principi seri: impedenza acustica, velocità, densità. Non come storie che ci fanno assimilare, vendute da uomini in nero, che si basano solo sul fatto che DEVI CREDERCI...

Vada quindi per la "sismologia secondo Danning", se non chè, Victor mi dispiace dirtelo sei arrivato tardi. Nel 1958 ormai si sapeva già quasi tutto di questa scienza, e non sei stato di certo tu ad inventarla...

Ti interessa? Leggi anche questo!!